© ApICS ® LLC 2000

Bridles function as tension amplifiers or line-speed pacers in metal strip process lines. The typical speed regulated bridle consists of several rolls each of which is driven by an individual power source. One of the rolls in the bridle is speed regulated. The other rolls in the bridle are operated as open-loop current followers that follow the current reference generated by the speed regulator (Figure 2). By slaving the helper-roll current references from the current reference generated by the speed regulator, each roll load-shares according to a predetermined ratio. The load-sharing ratios are a function of motor horse-powers, roll diameters [1], and gear-ratios. In some applications fine tuning of load-sharing is accommodated by individual gains on the current references.

In applications where low-speed bridle speed regulation can have a strong impact on the quality of the processed strip, it is imperative that the bridle helper-rolls and the speed-regulated roll operate with little or no relative deviation in speed. The following is a good example of an application that has such a requirement.

Assume that, because of space constraints, it is not possible to furnish accumulators in an independent tension leveling line. The line operates with a maximum line-speed of 1500 [ft/min] and is used to pre-process aluminum strip in preparation for painting. A requirement for continuous operation is the result of a market need to manufacture custom coil sizes for small volume buyers. A plausible solution is to operate the line at very low speeds (1 to 3 [ft/min]) and let the strip accumulate in a small loop when a coil change must be made. To avoid marking the strip in the leveler when operating at low speeds precise regulation of entry and exit bridle speed is required over a 1500:1 range. Precise entry and exit speed regulation at the low end of a large speed range is only possible if the entry and exit bridle helper-rolls and respective speed regulated rolls operate with no relative speed deviations.

A diagram of a typical 4-roll bridle is presented in Figure 1. Figure 2 shows a single-line diagram of the control structure of a 4-roll speed regulated bridle. In this example, the output of the speed minor loop (SML) of roll 4 provides the current references to the 4 current minor loops (CML’s). The SML regulates the speed feedback w₄ to match the speed reference w_REF

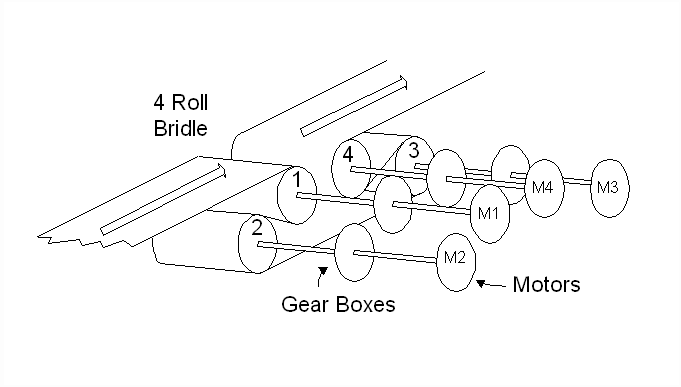
Figure 1. A Typical 4-Roll Bridle

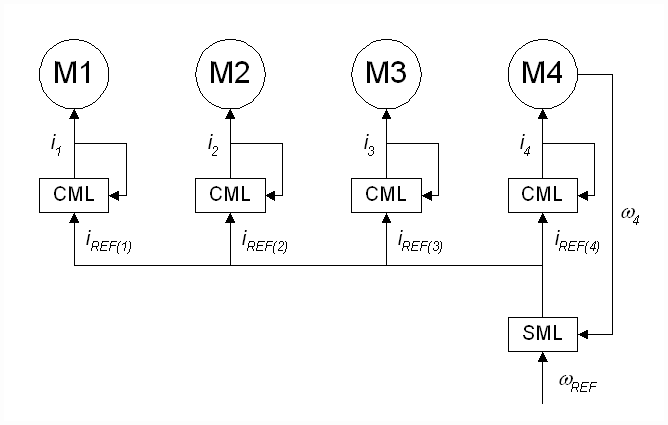
Figure 2. Single-Line Diagram of a Typical 4-Roll Bridle.

For many applications the control topology in Figure 2 is adequate. However, for extremely low-speed bridle applications such as that described above, this architecture will not provide satisfactory speed regulation. An explanation for this can be given in terms of the differences in system losses that occur from one bridle roll to the next.

The majority of system losses that occur in the drive trains and motors of a bridle can be lumped into the following friction classes: 1) viscous friction (B_V), 2) coulomb friction (B_C) 3) static friction or stiction (B_S), and 4) square-law windage losses (B_W). A popular equation ([2],[3]) combining these losses into an expression for the loss-torque in a drive is:

(1)

Plotting equation (1) results in a torque loss characteristic curve similar to Figure 3.

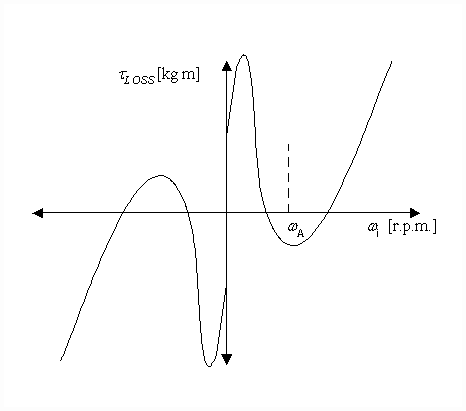
Figure 3. Bridle Roll Torque Loss Characteristic Curve

Each driven roll in the bridle will have differing values of B_V, B_C, B_S, and B_W. This results in differing torque loss characteristic curves from one helper-roll to the next.

Very low tension drops across bridle rolls can occur in some applications. This may require the drives to operate with very low drive currents, and, as a result of the extremely non-linear relationship between current and torque that transpires when DC drives operate in the discontinuous conduction region or AC drives operate with small I_q currents, a significant difference in the actual torque from the desired torque can result. This implies that a feed-forward current reference will not always produce the desired torque, and hence, the desired speed in the driven roll

The relationship between torque and speed in a bridle roll is given by equation (2) and the block diagram in Figure 4.

(2)

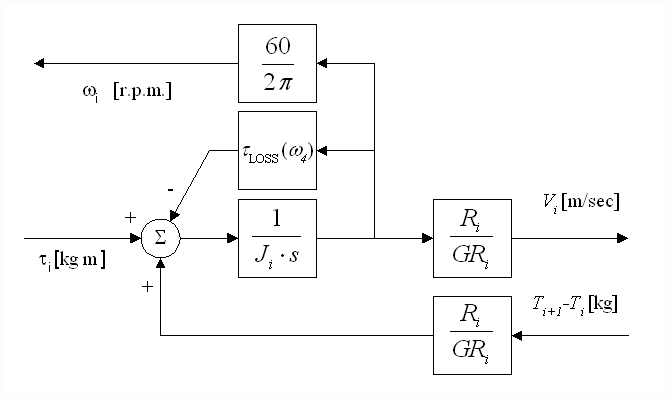
Figure 4. Block Diagram of Motor Torque-Balance Equation

If we assume that there is no strip attached to the driven roll (i.e. the strip tensions equal zero; T_i+1 = T_i = 0) and ‘n’ rolls are considered, it is clear from (2) that, for a common motor toque t_i and inertia J_i for all ‘n’ rolls, the speed of each roll will depend on the integral of the system losses. Assuming, as described above, the value of t_LOSS in each section differs, then as the ratio of t_LOSS to t_i increases, a more pronounced difference in speed between each driven roll will be observed.

From the above description of the typical bridle control topology it is clear that, at low speeds and low values of load torque {(T_i+1 - T_i)*R_i/GR_i)}, the ratio of t_LOSS to t_i can be high enough to create a condition where the speeds of the rolls in the bridle will differ significantly. This occurs as periodic abrupt excursions of speed from zero to a value greater than the line-speed set-point as the driven rolls move in and out of their respective static friction regions. For most metal application bridles, the speeds at which this occur are below 1 [m/min]. Figure 5 is a plot of measured currents and speeds for a 4 roll entry bridle in a tension leveler, configured as shown in Figure 2, with a line speed set-point of 2/3 [m/min] (2 [ft/min]).

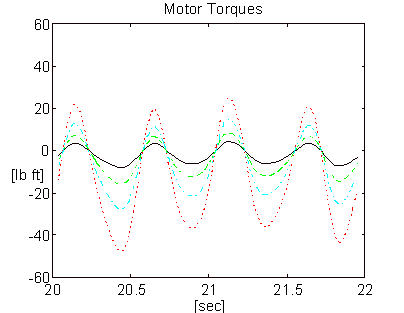
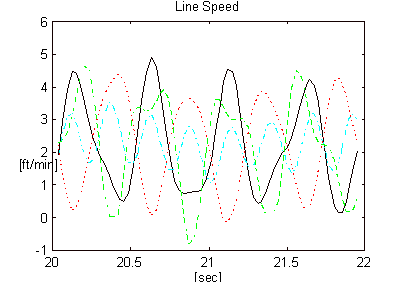
Figure 5. Measured Speeds and Currents of a 4-roll Bridle, Configured as Shown in Figure 2, Operating at a Low Speed.

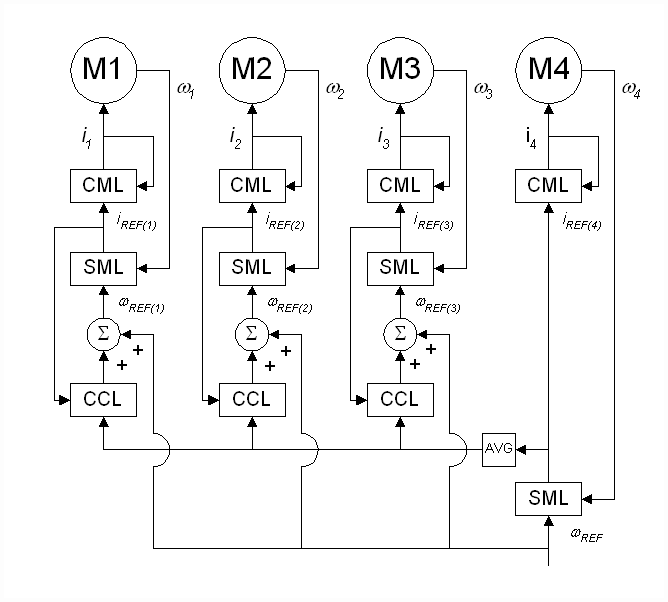
Figure 6. Proposed Bridle Control Topology

A significant improvement in low-speed speed regulation can be realized by cascading a current major loop with a speed-loop. A single-line diagram of the proposed control topology is presented in Figure 6. The output of the cascaded current-loop (CCL) provides a trim to the speed reference for the speed minor loop (SML) of each roll. The bandwidth of the CCL is designed such that it is at least 10 times less than the bandwidth of the CML. The assumption that the CML is an order of magnitude more responsive than the CCL ensures that the command reference to the CML will be approximately equal to the actual current. Given that the command reference to the CML is the output of the SML, the SML output can be used, in place of the measured current feedback, as the current feedback for the CCL. This is highly desirable in applications where the actual current feedback is small enough to be significantly corrupted by noise.

The improvement in speed regulation is realized by utilizing individual speed-loops for each driven roll. The speed-loops provide a way to compensate for the losses in each roll on a roll-to-roll basis and ensure that there will be little relative deviation in roll speed throughout the bridle over the full line speed range.

The remainder of the paper can be summarized as follows: Section two contains an analysis of the tuning strategy for the CCL. In addition, a description the de-coupling effect afforded by cascaded current-loops is provided. The third section presents results from a field trial, the fourth section provides some concluding remarks.

2.1 NOMENCLATURE

Equation (3) is commonly used to describe the dynamics associated with the conveyance of strip in metal strip process lines ([3], [4], [5], [6]). It is based on the principle of conservation of mass in a mass-flow system.

; (3)

where:

(4)

In Figure 7. an s-domain block diagram of equations (2-4) is presented. It includes the ‘hooks’ needed to couple multiple sections together, it does not include any strip material damping terms. Note that a rigorous representation of equations (2-4) requires the integrators in Figure 7 to be preset to their respective initial conditions.

For a given operating line velocity LS_i, an approximate linear representation of equations (1-3) can be obtained [7]. A block diagram of the linearized model is shown in Figure 8.

Figure 7. Block Diagram of a Strip Tension Zone

Figure 8. Linearized Block Diagram of a Strip Tension Zone

A linear s-domain block diagram approximation of a driven roll (Figure 9), as seen by a cascaded current-loop regulator, can be obtained by closing a speed-loop around the speed feedback w_i in Figure 8.

Figure 9. Plant Model Including the Speed-loop

Cascading four sections of the model in Figures 8 & 9 results in a block diagram (Figure 10) representation of the 4-roll bridle (Figures 1 & 6).

To simplify the analysis of the CCL several assumptions have been made. These assumptions are reflected in the following quantities from Figure 10:

1. The strip spring constants (K_T) for the strip between each roll in the bridle are identical.
1. The roll diameters (R), gear ratios (GR), and inertias (J) for each roll in the bridle are identical.
1. The bandwidth of each CML is high enough that in the frequency range of interest it behaves as a linear gain element (K_t).

3. DERIVATION OF AN APPROXIMATE CCL OPEN- LOOP TRANSFER FUNCTION, AND CCL TUNING

For a small-signal steady-state analysis of drive section two in Figure 10, the assumption is made that all transients from input disturbances have died out (i.e. V₁ and V₃ are constant). This best-case analysis assumes that the up-stream and down-stream load torques are balanced. Drive section two can then be represented as shown in Figure 11.

Figure 11. Steady State Representation of Section 2 in Figure 10.

The steady-state analysis of section two of the 4-roll bridle shown in Figure 11 yields the following open-loop transfer function (5) for the cascaded current-loop:

(5)

It can be shown that the bandwidth of the SML (without strip coupled to the bridle) is equivalent to (6). Note that the PI lead frequency must be less than the speed-loop bandwidth:

(6)

Substituting (6) into (5) yields:

(7)

If the speed-loop PI lead frequency is five times or more less than the speed-loop crossover (i.e. w_S < w_CO/5) the closed speed-loop may be modeled as a lag with a corner frequency equal to the speed-loop bandwidth (8):

(8)

Equation (7) reduces to:

(9)

Tuning the CCL regulator for a bandwidth of approximately 3/2 times the bandwidth of the speed minor loop and setting the CCL PI lead frequency at twice the desired current major loop bandwidth (or crossover frequency) yields the asymptotic Bode magnitude plot of Equation (9) seen in Figure 12.

Figure 12. Open Loop Asymptotic Bode Magnitude Plot Of CCL

Solving (9) for the gain term K_C2 that yields the open loop CCL crossover shown in Figure 12 yields:

(10)

A general tuning for the SML and CCL is:

The tuning derived in section 2.3 was derived under the assumption that the small signal response of the CCL is not affected by the dynamics of the coupled strip. Following is an analysis that demonstrates the validity of this assumption and the de-coupling effect afforded by the cascaded current-loop architecture.

Figure 13. Unbalanced Load Torque Application

Assume that a winder is coupled to an infinitely large mass by a section of strip with a strip spring constant equal to K_T, solving equations (2-4) results in the block diagram in Figure 13. The transfer function from current reference to current feedback of the CCL in this case is:

(11)

where

This analysis can be considered worst case in that the up-stream (T₂) and down-stream (T₀ = 0) load torques are completely unbalanced.

For realistic physical systems >> K_S w_S therefore the terms labeled A and B in (11) approximately cancel and can be ignored. The resulting asymptotic Bode magnitude plot of (11) is shown in Figure 14.

Figure 14. Open Loop Asymptotic Bode Magnitude Plot Of CCL

Solving (11) for the gain term K_C1 that yields the open loop CCL crossover shown in Figure 14 yields:

(12)

For physically realizable metal strip processing lines, . This implies that the CCL PI proportional gain terms expressed in (12) and (10) are essentially equivalent. That is, the gain term that was derived under the assumption that the small signal contribution from the up-stream and down-stream load torques cancel (best-case), is the same as the gain term for a system with load torques that are grossly imbalanced (worst-case). By inference, the effects of coupling the strip to the bridle affects the low frequency gain of the CCL, but has little affect on the CCL bandwidth, as shown in Figure 14.

In bridles configured using the architecture shown in Figure 2, the speed-loop bandwidth of the lumped bridle system is significantly limited by coupling effects resulting from the effective strip ‘springs’ that couple the rolls together. As the speed-loop bandwidth is increased, and by inference the loop gain increases, system noise is amplified by the PI controller and fed to the helper-rolls in their respective current references. The injection of this torque noise excites resonant modes in the bridle and, if excessive, can cause the entire machine to break into a violent oscillation. Filters can be employed on the current references to help alleviate this problem, at the risk of allowing damaging inter-roll tension transients during line accelerations and decelerations. Filtering or averaging the references of the helper-rolls CML’s, without the inclusion of inertia compensation, invariably leads to slippage in the bridle at these times.

The de-coupling effect and damping of system natural frequencies provided by SML’s in cascaded regulation schemes in strip transport systems is described in [7]. Wolferman [6] also alludes to these phenomena. The SML’s provide the helper-rolls with speed regulation to match the line speed reference, therefore, a running average that acts on the helper-roll CML references (see Figure 6) can be implemented without the adverse affects that result when using the architecture in Figure 2. Given that the torque references to the CCL’s is calculated to provide the drive with the torque required to maintain a desired load sharing profile throughout the bridle, the CCL reference can be considered a torque "offset" that is added to the torque required to overcome system losses and accelerate, decelerate, or maintain the roll speed, as commanded by the speed reference. The CCL references should ideally have little or no dynamic component. A running-average of the CCL reference is highly desirable.

Finally, the CCL should be tuned such that it has a bandwidth that is less than or at most equal to the bandwidth of the SML speed regulator. By applying this tuning strategy the outer current major loop will not swamp the inner speed loop, thereby allowing the speed loop to approximately compensate for system losses. The speed loop PI integrator will be charged by the vernier trim from the CCL to a value that approximates the current offset required to maintain the desired shaft torque that is being implicitly regulated by the CCL.

An O.E.M. tension-leveling line entry bridle on a tension-leveler was configured for operation with both architectures (Figures 2 and 6). The motor torque was calculated from armature current and filtered through a 2-pole Butterworth filter with a corner frequency of 62 [rad/sec] (10 [Hz]). The line speed was calculated from speed feedback [r.p.m.] and also filtered through a 10 [Hz] 2-pole Butterworth filter. 12 [mill] x 36 [in] aluminum strip was processed through the leveler at 2 [ft/min]. Figures 15 and 16 represent speed and torque for the architecture in Figure (2). Figures 17 and 18 represent speed and torque for the architecture in Figure (6).

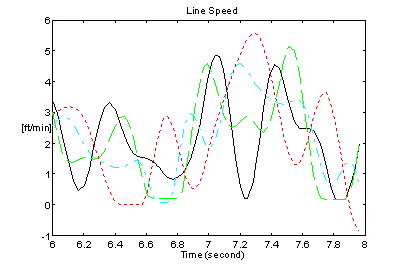
Figure 15. Line Speeds - Figure 2 Architecture

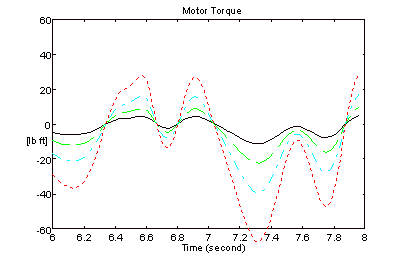
Figure 16. Motor Torques - Figure 2 Architecture

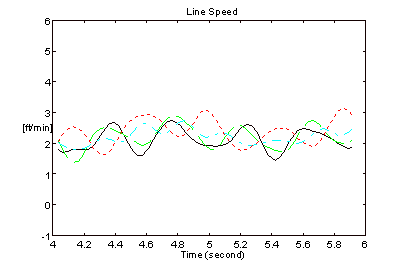
Figure 17. Line Speeds - Figure 6 Architecture

The bandwidth of the speed regulator driving roll 4 for the results in Figures 15 and 16 was approximately 10 [rad/sec]. The bandwidth of the speed regulators on all 4-rolls for the results in Figures 17 and 18 was approximately 30 [rad/sec]. The improvement in speed regulation is clearly evident when the CCL architecture is employed.

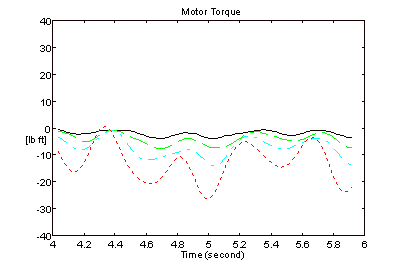
Figure 18. Motor Torques - Figure 6 Architecture

Significant improvements in bridle speed-loop bandwidths and speed regulation can be realized with the CCL architecture in multi-roll bridles. It is not unrealistic to expect a 3 to 4 fold increase in speed-loop bandwidth, drive-train integrity permitting, over those possible with the architecture presented in Figure 2. For bridle applications where excellent low-speed regulation is critical to product quality, the CCL architecture should be considered.

[1] Boulter, B.T., "Diameter Sizing of Rolls in Bridles That Utilize Powder Clutches ", I.E.E.E. I.A.S. Transactions , pp 2537-2540, March 1997.

[2] Hess, D.P., Soom, A. "Friction at a Lubricated Line Contact Operating at Oscillating Sliding Velocities" Journal of Tribology Transactions of the A.S.M.E. Vol 112, pp 147-152, 1992.

[3] Majd, V.J.. Simaan M. A., "A Continuous Friction Model For Servo Systems With Stiction", Proceedings of the 4^th I.E.E.E. Conference on Control Applications, Albany NY. 1996.

[4] Carter, W.C., "Reducing Transient Strains in Elastic Processes" , Control Engineering Mar. 1965. pp. 84-87.

[5] Lin, K., "WTS 6.0 A Computer-Based Analysis Program For Multi-Span Web Transport Systems", Oklahoma State University WHRC, 1994.

[6] Wolferman, W., "Tension Control of Webs - A Review of the Problems and Solutions in the Present and Future", Tab 15, Proceedings of the 3^rd International Web Handling Conference, Tab 17, Oklahoma State University June 1995.

[7] Boulter, B.T., "The Effect of Speed-loop Bandwidths and Line Speed on System Eigenvalues in Multi-Span Web Transport Systems", Proceedings of the 32^nd. I.E.E.E. I.A.S Conference, September 1997.